k-nearest neighbor

 KNN




The k-nearest neighbor algorithm is a supervised machine learning algorithm that can be used to solve both classification and regression problems.

Classification usage

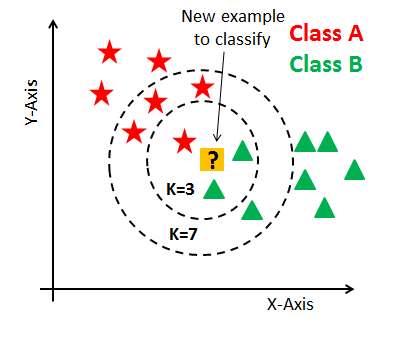
Let us understand the algorithm using the below figure where we have two classes of data points ( A and B). 



Source: www.kdnuggets.com


The first step is to determine the K value ( 'k' here is the number of nearest data points from the new data point). Let us take k = 3 as per the above figure. We can see that 2 out of 3 neighbors are from class B. So, in this case we go with the majority votes, i.e., the new data point will be classified as class B. We can use either Euclidean or Manhattan distance to get the nearest neighbor.


Regression usage

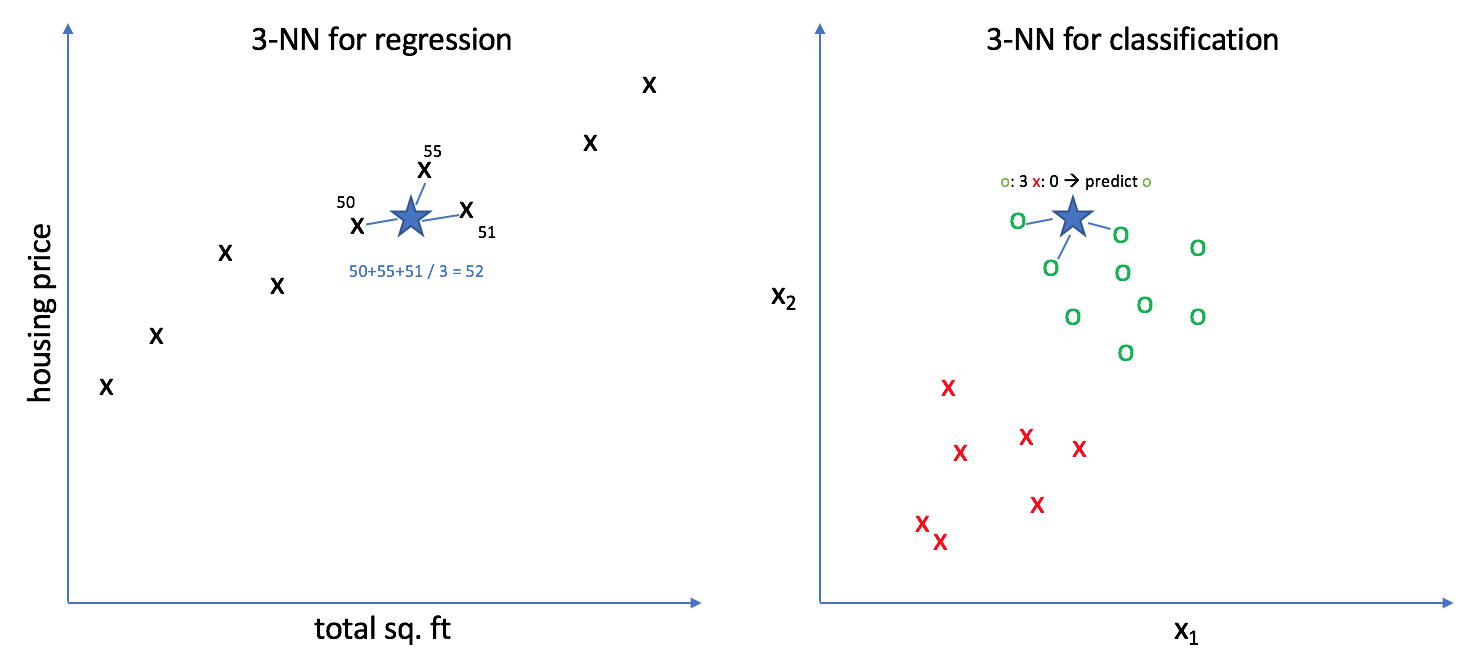
Below we can see the difference in the regression and classification usage. We will focus on the left figure for regression under this topic.


Source: www.jeremyjordan.me


Similar to the classification problem, here also we need to come up with a k value. If the k value is 3 and the new data point is the bigger blue star as in the figure, then predicted value for the new data point will be the mean of the 3 nearest data points. In this case it will be 52. The distance for the nearest neighbor is calculated with either Euclidean or Manhattan distance.

 

Selecting K value

Elbow method is used to basically get the value of k which will give the lowest WCSS(within cluster sum of square).
In this method a loop is run from k value 1 to n. For each value of K, the algorithm goes through all the steps that were mentioned above. For K =1, WCSS value will be very high and as the number of k value decreases the WCSS will decrease as we can see from below figure.





Comments

Post a Comment

Popular posts from this blog

Euclidean Distance and Manhattan Distance

Image
  Euclidean and Manhattan Distance Euclidean Distance and Manhattan Distance are the two distances that we generally use to find distance between two data points. Use of this distance can be seen in algorithms like KNN, Kmean and Hierarchical clustering. We can check if there are any similarities between the two data points with the help of these distances. Euclidean distance The smallest possible distance between any two points is named as euclidean distance. This distance is calculated based on Pythagoras theorem as shown in the below figure. Source:  cdn-images-1.medium.com This is the case for 2-D data.  For higher dimensions we can add the additional dimension. This is case for any number of dimensions. Euclidean distance is used where we calculate the distance between any two points in a straight line irrespective of whether there are any other data points in between them. Ex. when we google to check distance between Cochin and Delhi in case of flight we get a straight point from
Read more

K means clustering

Image
 K means clustering K-means  is a non-parametric method of clustering where we pre define the number of clusters(non-parametric means computation complexity depends in number of samples). It is an unsupervised machine learning technique. Source: miro.medium.com From the above figure, the algorithm finds the similarity between points and group them into clusters (green, blue and red in this case). Let us see what are the steps required and how the algorithm arrived at 3 clusters as above. Determine K value:  K value is basically how many centroids is needed for our data to form the best clusters. Here we can take any value for beginning.  Initialize K points (randomly) as cluster centers in the plane( K = 3 in this case) Find the distance between the points nearer to the centroids:  Here we can calculate the distance either using Euclidean and Manhattan Distance (Click here to know more about these distance). Based on the shortest distance from the centroids, clusters are formed. Sele
Read more