Euclidean Distance and Manhattan Distance

 Euclidean and Manhattan Distance



Euclidean Distance and Manhattan Distance are the two distances that we generally use to find distance between two data points. Use of this distance can be seen in algorithms like KNN, Kmean and Hierarchical clustering. We can check if there are any similarities between the two data points with the help of these distances.


Euclidean distance
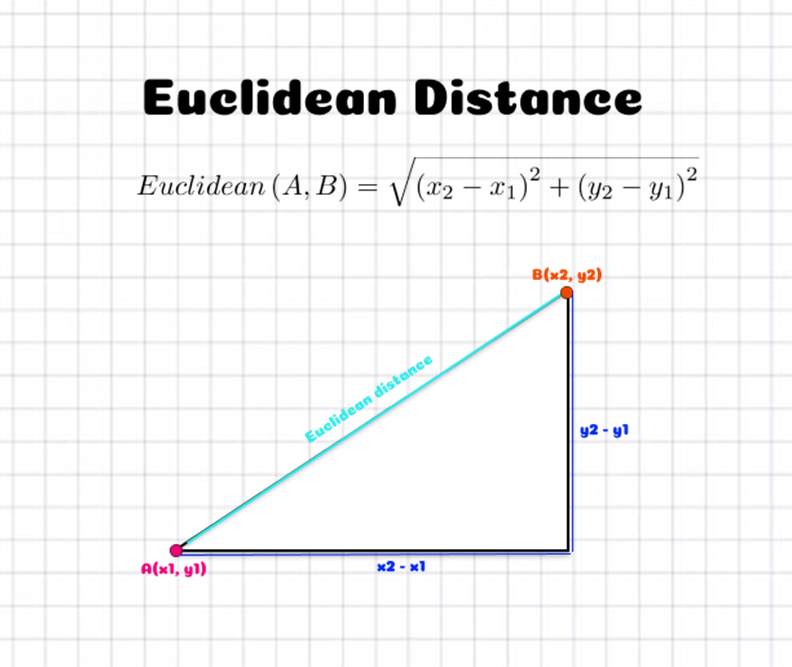
The smallest possible distance between any two points is named as euclidean distance. This distance is calculated based on Pythagoras theorem as shown in the below figure.

Source: cdn-images-1.medium.com

This is the case for 2-D data. 
For higher dimensions we can add the additional dimension.


This is case for any number of dimensions. Euclidean distance is used where we calculate the distance between any two points in a straight line irrespective of whether there are any other data points in between them. Ex. when we google to check distance between Cochin and Delhi in case of flight we get a straight point from Cochin to Delhi. 

Some properties:
  • It is symmetric, which means for all points 'a' and 'b', distance from a to b is same as b to a. The distance is independent of which point is taken as start or end.
  • It is always positive, which means distance between any two points will always be positive.
  • It follows triangle inequality, which means for every three points a, b, and c
 
Source: cheenta



Manhattan Distance

The distance between two points that is measured along the axis at right angles is called Manhattan distance.
In any modern structured city where all the houses are constructed in a proper block fashion, the distance between one house to the other is calculated via road (following the road pattern). We are not taking a shortcut distance which might even pass through other houses in between. 


In general we need to try using both the distance in the machine learning use cases and do cross validation to check which is working best for our model.




References:
  1. Wikipedia
  2. YouTube Channel - sentdex
  3. YouTube Channel - Krish Naik



Comments

Post a Comment

Popular posts from this blog

Ensemble Technique 2 : AdaBoost

Image
 AdaBoost AdaBoost or Adaptive Boosting is a boosting technique that is used as an Ensemble Method in Machine Learning. In this algorithm, the weights are re-assigned at each and every instances with higher weight for wrongly classified instances. The main motive behind this algorithm is to convert the weak learners to strong learners. Source:  miro.medium.com Boosting Technique As we can see from the above figure, suppose the original data is D1 and the trained classifier seen below is a base learner BL1(say). BL1 can be any model/algorithm provided with a sample of data to train. After training the model, when the original data is used to validate the model, the incorrectly classified records are further treated by moving them to a next base learner (BL2). Now the BL2 will be trained with those wrong classified records and further if they classify some more records incorrectly then again a new base learning is created (BL3) and this process continues till we specify some limits to th
Read more

Forecast Accuracy Metrics

Image
 Forecast Accuracy Metrics We will be discussing here about the most commonly used forecast accuracy metrics mentioned below: Forecast bias MAD MAPE MSE RMSE MPE Forecast Bias This metric will help us in understanding whether the model has over estimated or under estimated. If the value is positive then its overestimation and if its negative then underestimation.  In order to get bias as a % of sales, we have Forecast Bias %                                                                             fig:  relexsoumtions                                    If the value is more than 100 % then its an over forecast and if its less than 100% its under forecast. It is important metric in demand forecasting as it will tell us the over or under supply at the central warehouse or distribution centers. It does not give information on quality of detailed level of forecast. Target is to achieve a 1 or 100% and the number -/+ tells the deviation.        2. Mean Absolute Deviation (MAD) This metrics
Read more