Decision Tree

 Decision Tree



A decision tree is a decision support tool that uses a tree-like model of decisions and their possible consequences, including chance event outcomes, resource costs, and utility. (Source: Wikipedia)

 
Decision tree can be used in solving classification as well as regression problems. In most of the cases for classification purpose, we use decision tree. In this algorithm a tree structured classifier is generated by the model. 
In a decision tree, there are 2 nodes that we need to consider. 
  1. Decision node (nodes with further extension to another node)
  2. Leaf node (last node in tree which provides final class labels)
The target of the algorithm is to reach the leaf node asap. Entire data is provided to the root node(decision node) and where splitting action happens.

To construct a decision tree, there is an algorithm called as ID3 (Iterative Dichotomiser 3). First step is to select the right attribute/feature for splitting the decision tree. For this we need to use the entropy technique. This point is very important because if we are able to select the right feature from the beginning, we can reach to the leaf node quickly which is the motive of decision tree algorithm.


Entropy
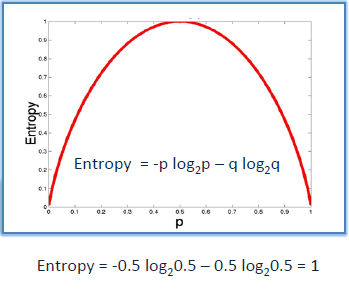
It helps in measuring the purity of the split. Pure split means either we are getting Yes or No, there should not be any combination of both. So to attain a pure split, the splitting continues (till we reach the leaf node). Entropy value is between 0 and 1.

Source: saedsayad


p = percentage of positive class
q = percentage of negative class

In the above image, we can see there is 50-50 probability of Yes and No. This considered as the worst split(complete impure split) where entropy value will be equal to 1. For pure split, the entropy value will be 0(either a Yes or No). That is where we stop splitting because we have reached leaf node. Lower entropy better the feature splitting.
Source: saedsayad

For example, from the above calculation, if there are any feature that is giving better entropy value (lower than 0.94) will be selected for further splitting instead of the "PlayGolf".  Summation of entropy of all values from root to leaf node need to be done which is done by information gain.

Information Gain
In the beginning, I have mentioned entropy is used only to get the best split or to find the purity of split, But now we have number of split within a tree. So, in that case we need to select a particular pattern. Here comes the concept of information gain. Information Gain means we will compute the average of all the entropy based on the split.
 

Source: miro.medium.com


T is the subset
Tv is the subset after splitting

Higher the information gain, that pattern(or structure of decision tree) of splitting is selected in the case of IG.


Gini Impurity
We have studied how entropy calculate the purity of split and here we have Gini impurity which do the same work. But most of the time GI is better than entropy.

Source: media.geeksforgeeks.org


p = probability of positive value + probability of negative value

Impure split will give the maximum GI of 0.5

Source: media.geeksforgeeks.org

Gini entropy is used in majority of cases because this is computationally more efficient than entropy. Because in entropy we have log2 in the formula which will take time for the algorithm to compute. Hence GI takes shorter period of computation time.


Decision Tree split for Numerical Features
So far we have mentioned about the data with categorical features. Now let us see how the algorithm works when the features of data are numerical in nature. To split this type of data few steps need to be followed.

  1. Sorting all the values in ascending order
  2. Take a threshold value which is the lowest among all(that is in the first position after ordering) eg. 2.4. If the value is less or equal than 2.4 then we take that split as Yes and greater than 2.3 as No. 
  3. Then we take next split, we take threshold as the next number(eg, 3.4)
  4. Calculation of entropy/gini index and information gain is calculated. The split giving best value is selected.

The issue with this computation is the time complexity. This will increase when we have more data.



References:
  1. YouTube Channel - Krish Naik
  2. Wikipedia

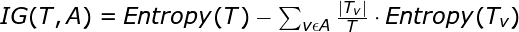
Comments

Post a Comment

Popular posts from this blog

Euclidean Distance and Manhattan Distance

Image
  Euclidean and Manhattan Distance Euclidean Distance and Manhattan Distance are the two distances that we generally use to find distance between two data points. Use of this distance can be seen in algorithms like KNN, Kmean and Hierarchical clustering. We can check if there are any similarities between the two data points with the help of these distances. Euclidean distance The smallest possible distance between any two points is named as euclidean distance. This distance is calculated based on Pythagoras theorem as shown in the below figure. Source:  cdn-images-1.medium.com This is the case for 2-D data.  For higher dimensions we can add the additional dimension. This is case for any number of dimensions. Euclidean distance is used where we calculate the distance between any two points in a straight line irrespective of whether there are any other data points in between them. Ex. when we google to check distance between Cochin and Delhi in case of flight we get a straight point from
Read more

Ensemble Technique 2 : AdaBoost

Image
 AdaBoost AdaBoost or Adaptive Boosting is a boosting technique that is used as an Ensemble Method in Machine Learning. In this algorithm, the weights are re-assigned at each and every instances with higher weight for wrongly classified instances. The main motive behind this algorithm is to convert the weak learners to strong learners. Source:  miro.medium.com Boosting Technique As we can see from the above figure, suppose the original data is D1 and the trained classifier seen below is a base learner BL1(say). BL1 can be any model/algorithm provided with a sample of data to train. After training the model, when the original data is used to validate the model, the incorrectly classified records are further treated by moving them to a next base learner (BL2). Now the BL2 will be trained with those wrong classified records and further if they classify some more records incorrectly then again a new base learning is created (BL3) and this process continues till we specify some limits to th
Read more

Forecast Accuracy Metrics

Image
 Forecast Accuracy Metrics We will be discussing here about the most commonly used forecast accuracy metrics mentioned below: Forecast bias MAD MAPE MSE RMSE MPE Forecast Bias This metric will help us in understanding whether the model has over estimated or under estimated. If the value is positive then its overestimation and if its negative then underestimation.  In order to get bias as a % of sales, we have Forecast Bias %                                                                             fig:  relexsoumtions                                    If the value is more than 100 % then its an over forecast and if its less than 100% its under forecast. It is important metric in demand forecasting as it will tell us the over or under supply at the central warehouse or distribution centers. It does not give information on quality of detailed level of forecast. Target is to achieve a 1 or 100% and the number -/+ tells the deviation.        2. Mean Absolute Deviation (MAD) This metrics
Read more